Processingで三角関数のサイン、コサインを使ったアニメーション

三角関数は数学でやったことはあると思いますが、三角関数の円運動は高校物理で詳しく習うと思います。プログラミングの世界でもこの三角関数を使う場合があります。
三角関数は三角比の値を求めるもので、ベクトルを考える上で必要な角度を求めることができます。

Processingではこの三角関数を使って波形のような滑らかな動きのアニメーションをさせたり、またサイン、コサイン、タンジェントの三角比から座標を計算して円運動をさせることがあります。

まずはざっくりおさらいとしてサイン、コサイン、タンジェントの計算式。

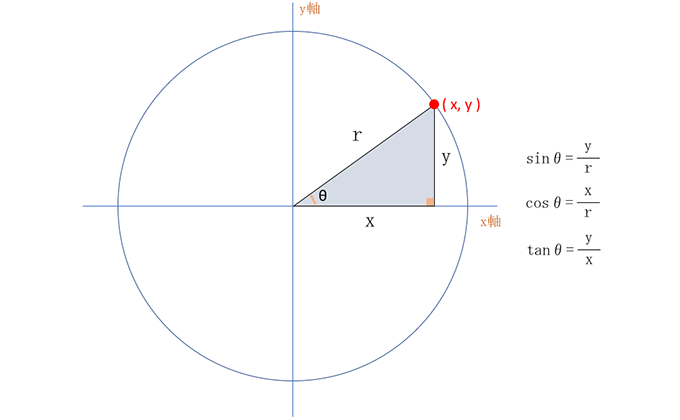
そして、Processingのdraw関数でのアニメーションで角度から求められる座標を計算して波形の曲線の動きを表現します。
タンジェントはそんなに使うことはないと思うので、ここでは説明を省きます。

Processingのsin関数とcos関数は、円の半径と角度からサインとコサインの三角比を求めることができる関数となります。
ですので円運動をさせる場合、円の半径と角度を決めればあとはsin関数とcos関数でx座標とy座標が導き出せます。

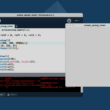
円運動

int eSize = 20; //オブジェクトのサイズ
float angle = 0.0; //角度
float a = 100.0; //amplitude(振幅)　円の半径
float x = 0.0; //x座標
float y = 0.0; //y座標
 
void setup() {
  size(640, 400);
  frameRate(50);
}
  
void draw() {
  background(240);
  translate(width/2, height/2);
  angle += 0.1; //角度をつけていく
   
  x = a*cos(angle); //x座標の計算
  y = a*sin(angle); //y座標の計算
  fill(0);
  ellipse(x, y, eSize, eSize);
}

変数aはamplitude(振幅)としてdraw関数で表現される円の半径となります。
drawの中でangle（角度）をつけていき、その角度をx座標、y座標のサイン、コサインから導き出せる座標の計算をおこないます。
あとはellipseで描いているオブジェクトの座標に当てはめれば、計算された座標から円運動が表現できます。

xとyのサインとコサインを反対にすると、反時計方向の円運動となります。

サイン、コサインの円運動は角度の変化から-1から1の間を行き来するものとなります。

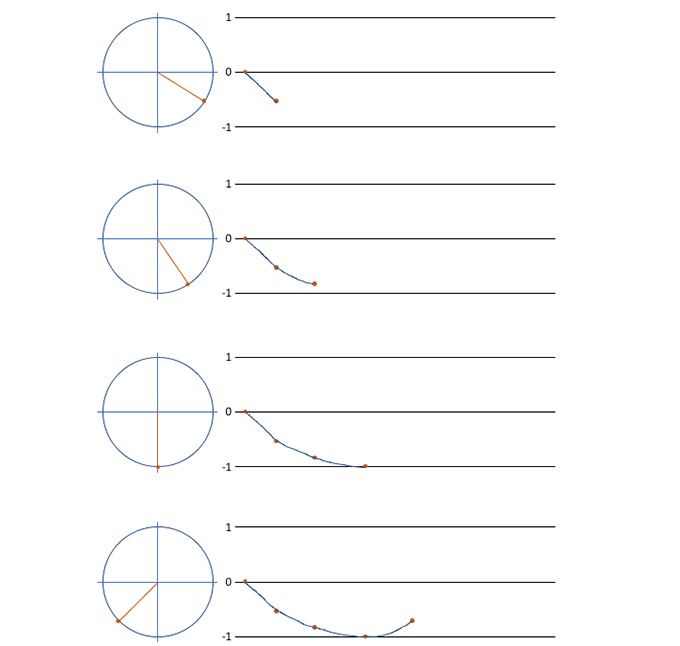
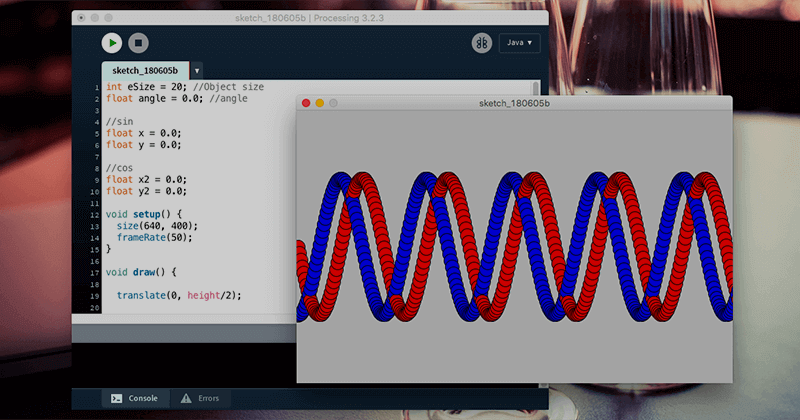
ですので普通の波形のアニメーションでは以下のようになります。

波形

/* sin、cos 波形 */
float angle = 0.0; //角度
 
//sin
float x = 0.0;
float y = 0.0;
 
//cos
float x2 = 0.0;
float y2 = 0.0;
 
void setup() {
  size(640, 400);
  frameRate(50);
}
  
void draw() {
  //background(255);
  translate(0, height/2);
   
  //sin(red)
  x += 2.0;
  y = 100*sin(angle);
  fill(255, 0, 0);
  ellipse(x, y, eSize, eSize);
   
  //cos(blue)
  x2 += 2.0;
  y2 = 100*cos(angle);
  fill(0, 0, 255);
  ellipse(x2, y2, eSize, eSize);
   
  angle += 0.1; //角度をつけていく
}

サインが赤、コサインが青としてみました。
-1から1の間の動きは変わりません。